Resonance Mirror

In the last chapter we mentioned the fact that only the fractional part of the spin tune is measurable. Similar to the fact that a traveler going $\frac{3\pi}{2}$ around a circle ends at the same spot his fellow does when going around $\frac{\pi}{2}$ in the other direction, we can't be a priori sure when observing a ``resonant'' frequency that this isn't just the mirror frequency of the resonance. 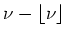According to the Nyquist Theorem we can only measure how much below or above we are from the half-integer, but not on which side or in mathematical terms, does the measured frequency correspond to $\nu -\lfloor\nu\rfloor$ or $\nu +1-\lfloor\nu\rfloor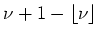$. For example the frequency 500 kHz corresponds to a beam energy of 2.372 GeV but also to the mirror energy at 2.475 GeV; this ambiguity is resolved in the following way:

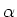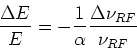The energy of the beam can be slightly varied using a different RF main frequency. At SLS the RF main frequency is 500 MHz. Beam energy and RF main frequency are related by the momentum compaction factor $\alpha$:

$$\frac{\Delta E}{E}=-\frac{1}{\alpha}\frac{\Delta\nu_{RF}}{\nu_{RF}}$$ (52)

Therefore a change in the RF main frequency will lead to a change in beam energy. If the RF main frequency is changed to a lower value, the beam energy will rise. If the resonant frequency increases as well it is the ``real'' resonance; if however the resonant frequency decreases, it is the mirror resonance and vice-versa. Thus this procedure always requires a second measurement of the resonant frequency.