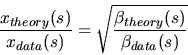The Beta-Beat

If one assumes that the beam position of the theoretical calculation and the measurements have to lie over each other and the tune, the phase and the kick are measured correctly, then a difference between theoretically predicted and measured $\beta$-function (i.e. the beta-beat) can be calculated. Taking equation 6 one receives:

$$\frac{x_{theory}(s)}{x_{data}(s)}=\sqrt{\frac{\beta_{theory}(s)}{\beta_{data}(s)}}$$ (8)

And this then leads to a value for the actual $\beta$-function of the storage ring at any given position $s$:

$$\beta(s)=\beta_{theory}(s)\cdot\left(\frac{x_{data}(s)}{x_{theory}(s)}\right)^{2}$$ (9)

A plot of this actual $\beta$-function compared to the theoretical $\beta$-function is given in figure 19.

Figure 19: Comparison of the $\beta$-functions of measured data with theoretical prediction.

Another interesting discovery are the two spikes at BPM 28 (bpm_05sd) and BPM 59 (bpm_10me). It turned out that BPM 59 (bpm_10me) was turned off during measurement (because of a malfunction) and BPM 28 (bpm_05sd) was giving the wrong readout due to insufficient settings. As a consequence of this measurement these errors were corrected.