... paper¹

Copies of this paper can be found online at http://www.simonleemann.ch/work.html or can be obtained by sending e-mail to the author at sl@simonleemann.ch

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... SLS²

Swiss Light Source SLS, Paul Scherrer Institute PSI, Villigen, Switzerland

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... zero³

This refers to a simple model. Actually one should find a periodic solution of the Thomas-BMT equation by integrating around the periodic closed orbit. Similar to the fact that horizontal and vertical displacements from the design orbit lead to a periodic solution for the orbital motion (the closed orbit) there is a periodic solution of the Thomas-BMT equation on the closed orbit for the spin vector 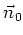$\vec{n}_0$ which obeys 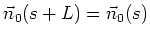$\vec{n}_0(s+L)=\vec{n}_0(s)$. This more detailed approach shows that in a perfectly flat machine 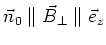$\vec{n}_0 \parallel \vec{B}_{\perp} \parallel \vec{e}_z$ but in real machines 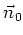$\vec{n}_0$ has slight deviations from 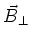$\vec{B}_{\perp}$ which in fact determines the equilibrium polarization level. [10]

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... fields.⁴

However one must keep in mind that in storage rings typical field errors (from magnet misalignment for example) are proportional to the beam energy 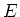$E$, i.e. after passing through an error field the electron's angular deflection is independent of 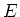$E$. Yet for the spin the dependency is different: The spin vector is perturbed by an angle 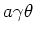$a\gamma\theta$ which is proportional to 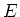$E$. Hence the higher the beam energy, the more sensitive the electrons are to errors and therefore the more vulnerable the beam is to depolarizing effects. This is well demonstrated when comparing typical levels of polarization at LEP (11% at 50 GeV) and at SPEAR (90% at 3.7 GeV). [12]

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... phase)⁵

Keep in mind that in equation 11 the spin vector 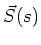$\vec{S}(s)$ was a function of the traveled distance of the electron whereas here it is a function of time 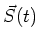$\vec{S}(t)$ which is more practical since a time-dependent field 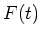$F(t)$ has been taken into account. Notice also that equation 12 presented solutions for the spin motion in the electron's rest frame; the solutions here are in the lab frame which is the frame of interest when describing spin motion under influence of a kicker magnet field.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... obtained⁶

Note that this is only possible for the equilibrium level. Using this method it is not possible to measure the degree of polarization at any given time, i.e. outside of the equilibrium state. This would still require a polarimeter.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... 500 kHz⁷

Note that the mentioned sweep would require almost 28 hours while a machine shift at SLS is only 8 hours! Therefore we normally first swept at high speeds over a large interval; when a resonance is found the sweeping interval is narrowed and the sweep speed lowered to increase resolution. This is an iterative and more efficient procedure but still a very time consuming task. Once we depolarized the beam at the resonant frequency we had to wait for polarization to build up in the beam again before we could start the next sweep. Remember that the characteristic polarization time at SLS is more than a half hour!

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... current⁸

The mentioned linearity is valid in the area of 50-150 mA beam current where our experiments take place, see [14].

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.