



Next: Experimental Approach and Equipment
Up: Introduction
Previous: Beam Excitation and Resonances
Contents
In chapter 2.2 it was shown that due to synchrotron radiation an electron beam in a storage ring will polarize with a certain characteristic time constant 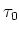 to the maximum level of polarization
to the maximum level of polarization 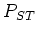 . In chapter 2.4 depolarizing mechanisms were introduced. It was also mentioned that field errors had less influence on the level of polarization in low-energy machines like SLS, thus high polarization levels should be achievable at SLS. In this section a simple model for the equilibrium polarization build-up at SLS will be discussed.
. In chapter 2.4 depolarizing mechanisms were introduced. It was also mentioned that field errors had less influence on the level of polarization in low-energy machines like SLS, thus high polarization levels should be achievable at SLS. In this section a simple model for the equilibrium polarization build-up at SLS will be discussed.
Polarization build-up at SLS is described by equation 5:
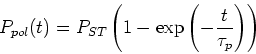 |
(38) |
with 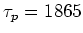 s at the nominal energy of 2.4 GeV. Depolarizing effects are expected to show an exponential decay of the polarization:
s at the nominal energy of 2.4 GeV. Depolarizing effects are expected to show an exponential decay of the polarization:
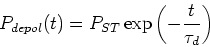 |
(39) |
The equilibrium state between the polarization build-up due to spin-flip radiation and depolarizing effects due to photon emission is described again by an exponential build-up:
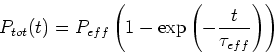 |
(40) |
where
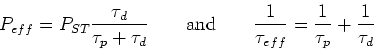 |
(41) |
Expecting an equilibrium polarization level of 80% at SLS one can derive the characteristic depolarization time as well as the equilibrium polarization build-up time from equation 41. In the example shown in figure 5 the following values have been used:
![\includegraphics [width=1.0\textwidth]{figures/polbuildup}](img109.gif)
Figure 5:
A model for the effective polarization build-up in the SLS storage ring. The time interval shown is ten hours which corresponds to typical beam lifetimes.
It is important to note that depolarizing effects have a very long characteristic time 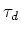 compared to polarization build-up
compared to polarization build-up 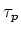 (in this situation) leading to high polarization values.
(in this situation) leading to high polarization values.




Next: Experimental Approach and Equipment
Up: Introduction
Previous: Beam Excitation and Resonances
Contents
Simon Leemann
2002-03-15
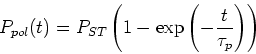
![]() s at the nominal energy of 2.4 GeV. Depolarizing effects are expected to show an exponential decay of the polarization:
s at the nominal energy of 2.4 GeV. Depolarizing effects are expected to show an exponential decay of the polarization:
![\includegraphics [width=1.0\textwidth]{figures/polbuildup}](img109.gif)
![]() compared to polarization build-up
compared to polarization build-up ![]() (in this situation) leading to high polarization values.
(in this situation) leading to high polarization values.