



Next: Beam Excitation and Resonances
Up: Introduction
Previous: Depolarizing Effects
Contents
Using a very strong kicker magnet the spin ensemble could be tilted into the horizontal plane during one pass through the kicker field, but without spin diffusion this does not lead to beam depolarization. However over many revolutions around the ring it is possible to tilt the mean spin vector bit by bit to the horizontal plane by using time-varying magnetic fields in resonance with the electron's spin revolutions. This procedure is depicted in figure 4.
Recalling equation 20 we can calculate the opening angle of the precession cone after 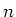 revolutions:
revolutions:
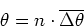 |
(21) |
and since we know that depolarization is reached by tilting the mean spin vector into the horizontal plane (over a time which is long enough to allow spin diffusion), we can define the depolarization time 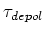 :
:
and therefore, we derive:
![\begin{displaymath}
\tau_{depol} = \frac{\pi}{2} \cdot \left[\frac{2}{\pi}~\frac...
...ft(B_{kick}\cdot l\right) \right]^{-1} \cdot \frac{1}{\nu_{0}}
\end{displaymath}](img74.gif) |
(23) |
In the case of the SLS storage ring this leads to:
![\begin{displaymath}
\tau_{depol}\left[s\right] \approx 3.48 \cdot 10^{-6} \cdot \frac{1}{B_{kick} \cdot l\left[ Tm\right]}
\end{displaymath}](img75.gif) |
(24) |
If we require depolarization time not to be longer than a second it can be derived from equation 24:
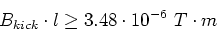 |
(25) |
Such values can be well achieved with the multi-bunch feedback kicker magnets installed at SLS (
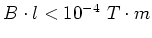 ).
).




Next: Beam Excitation and Resonances
Up: Introduction
Previous: Depolarizing Effects
Contents
Simon Leemann
2002-03-15
![\includegraphics [width=0.8\textwidth]{figures/resdepol}](img61.gif)
![$\displaystyle n \cdot \left[\frac{2}{\pi}~\frac{ea}{m_ec}\cdot \left(B_{kick}\cdot l\right) \right]$](img70.gif)
![$\displaystyle \tau_{depol} \cdot \nu_{0} \cdot \left[\frac{2}{\pi}~\frac{ea}{m_ec}\cdot \left(B_{kick}\cdot l\right) \right]$](img71.gif)
![\begin{displaymath}
\tau_{depol} = \frac{\pi}{2} \cdot \left[\frac{2}{\pi}~\frac...
...ft(B_{kick}\cdot l\right) \right]^{-1} \cdot \frac{1}{\nu_{0}}
\end{displaymath}](img74.gif)
![\begin{displaymath}
\tau_{depol}\left[s\right] \approx 3.48 \cdot 10^{-6} \cdot \frac{1}{B_{kick} \cdot l\left[ Tm\right]}
\end{displaymath}](img75.gif)